Resampling Without Replacement

Introduction

Sampling without replacement implies that elements of a population can be chosen only once in one sample. There are different techniques of sampling without replacement, including:

• simple random sampling
• random sampling with unequal probabilities
• stratified sampling
• balanced sampling (a special case of stratified sampling)
• permutation sampling
• k-fold sampling
• leave-p-out sampling

In this article, we show how to draw repeated samples without replacement from a population by using the functions implemented in resampling.

For further information on the sampling techniques, see Sampling without replacement.

Setup

Loading

Firstly, we need to load resampling and other needed R packages:

#resampling
library(resampling)

#Packages for visualisation
require(ComplexHeatmap, quietly = TRUE)
require(grid, quietly = TRUE)
require(RColorBrewer, quietly = TRUE)

Seed

Then, we set a seed for the random number generation (RNG). In fact, different R sessions have different seeds created from current time and process ID by default, and consequently different simulation results. By fixing a seed we ensure we will be able to reproduce the results of this vignette. We can specify a seed by calling ?set.seed.

#Set a seed for RNG
set.seed(
  #A seed
  seed = 5381L,                   #a randomly chosen integer value
  #The kind of RNG to use
  kind = "Mersenne-Twister",      #we make explicit the current R default value
  #The kind of Normal generation
  normal.kind = "Inversion"       #we make explicit the current R default value
)

Resampling Without Replacement

The available methods for taking repeated samples without replacement can be listed through the ?listAvailableSamplingMethods function call, setting the input argument to 'rswor'. ?listAvailableSamplingMethods returns a table with two columns:

• id: the id of the sampling method, to be used in the function calls
• name: the name of the sampling method

#list sampling methods
sampling.methods = listAvailableSamplingMethods(x = 'rswor')

#print in table
knitr::kable(x = sampling.methods)

id	name
rswor	random sampling without replacement
srswor	simple random sampling without replacement
stratified_rswor	stratified random sampling without replacement
balanced_rswor	balanced random sampling without replacement
permutation	permutation sampling
kfolds	random k-fold sampling
stratified_kfolds	stratified k-fold sampling
balanced_kfolds	balanced k-fold sampling
leave_p_out	leave-p-out sampling
leave_one_out	leave-one-out sampling

The name of the resampling functions can be retrieved by calling ?listResamplingFunctionNames.

#list resampling function names
resampling.function.names = listResamplingFunctionNames(x = 'rswor')

#print in table
knitr::kable(x = resampling.function.names)

id	name
rswor	repeatedSampleWithoutReplacement
srswor	repeatedSimpleRandomSampleWithoutReplacement
stratified_rswor	repeatedStratifiedSampleWithoutReplacement
balanced_rswor	repeatedBalancedSampleWithoutReplacement
permutation	repeatedPermutationSample
kfolds	repeatedRandomKm1Folds
stratified_kfolds	repeatedStratifiedKm1Folds
balanced_kfolds	repeatedBalancedKm1Folds
leave_p_out	repeatedLeavePOutSample
leave_one_out	repeatedLeaveOneOutSample

Each function is documented. To learn more about a specific method it is possible to use the ? operator. For example, let’s check the function ?repeatedSimpleRandomSampleWithoutReplacement.

#See documentation
?repeatedSimpleRandomSampleWithoutReplacement

From the documentation, we can see that the function accepts 3 arguments in input:

• k: the number of repeated samples to generate
• N: the population size
• n: the sample size

Simple Random Sampling

In resampling via simple random sampling (SRS), simple random samples without replacement are repeatedly taken from the population.

The function implementing this sampling scheme is ?repeatedSimpleRandomSampleWithoutReplacement, which accepts 3 arguments:

• k: the number of repeated samples to generate
• N: the population size
• n: the sample size

#Simple random sampling without replacement
repeatedSimpleRandomSampleWithoutReplacement(
  k = 2,
  N = 10,
  n = 8
)
#> [[1]]
#> [1]  1  9  7  2  4  3  6 10
#> 
#> [[2]]
#> [1] 9 8 1 7 4 5 6 3

Instead of using ?repeatedSimpleRandomSampleWithoutReplacement, we can take repeated samples by using the ?resample function.

#Simple random sampling without replacement
obj = resample(
  x = 10,
  n = 8,
  k = 2,
  method = 'srswor'
)

#Print
print(obj)
#> 
#> 2 samples taken from a population of 10 elements by using simple random
#> sampling without replacement.
#> 
#>   sampleNumber          sample sampleSize holdoutSize
#> 1            1 2, 3, 9, 5, ...          8           2
#> 2            2 2, 10, 8, , ...          8           2

#Samples
getSamples(obj)
#> [[1]]
#> [1] 2 3 9 5 7 4 6 1
#> 
#> [[2]]
#> [1]  2 10  8  1  6  4  3  7

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> [1]  8 10
#> 
#> [[2]]
#> [1] 5 9

#Plot
plot(x = obj)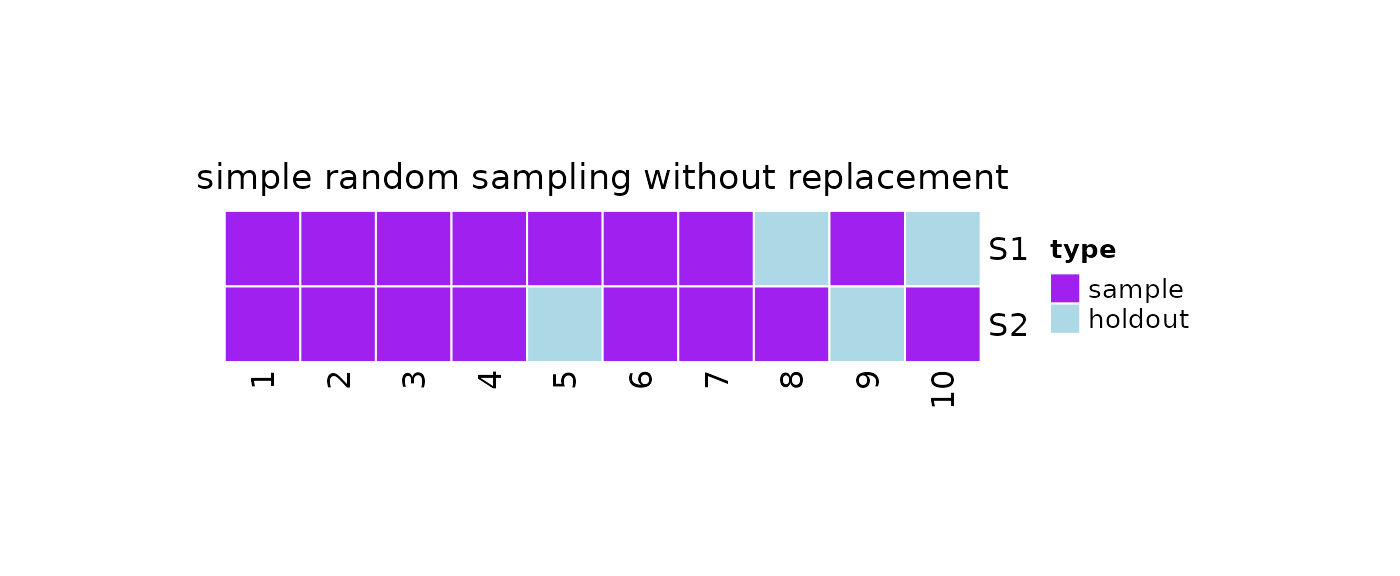

Random Sampling With Unequal Probability

We can use ?repeatedSampleWithoutReplacement to draw repeated samples without replacement with unequal probability. From the documentation, we can see that the function accepts 4 arguments in input:

• k: the number of repeated samples to generate
• N: the population size
• n: the sample size
• prob: an optional vector of probabilities for obtaining the population elements

For example, let’s assume our population of interest has 10 elements, and that the first 3 elements have an higher chance of being selected.

#Random sampling without replacement
repeatedSampleWithoutReplacement(
  k = 2,
  N = 10,
  n = 5,
  prob = c(rep(3,3), rep(1,7))
)
#> [[1]]
#> [1]  3  7 10  2  1
#> 
#> [[2]]
#> [1] 7 2 1 9 3

We can take repeated samples by using the ?resample function and setting method = 'rswor'.

#Random sampling without replacement
obj = resample(
  x = 10,
  n = 5,
  k = 2,
  method = 'rswor',
  prob = c(rep(3,3),rep(1,7))
)

#Print
print(obj)
#> 
#> 2 samples taken from a population of 10 elements by using random
#> sampling without replacement.
#> 
#>   sampleNumber          sample sampleSize holdoutSize
#> 1            1 7, 3, 6, 2, ...          5           5
#> 2            2 6, 1, 2, 3, ...          5           5

#Samples
getSamples(obj)
#> [[1]]
#> [1] 7 3 6 2 1
#> 
#> [[2]]
#> [1] 6 1 2 3 8

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> [1]  4  5  8  9 10
#> 
#> [[2]]
#> [1]  4  5  7  9 10

#Plot
plot(x = obj)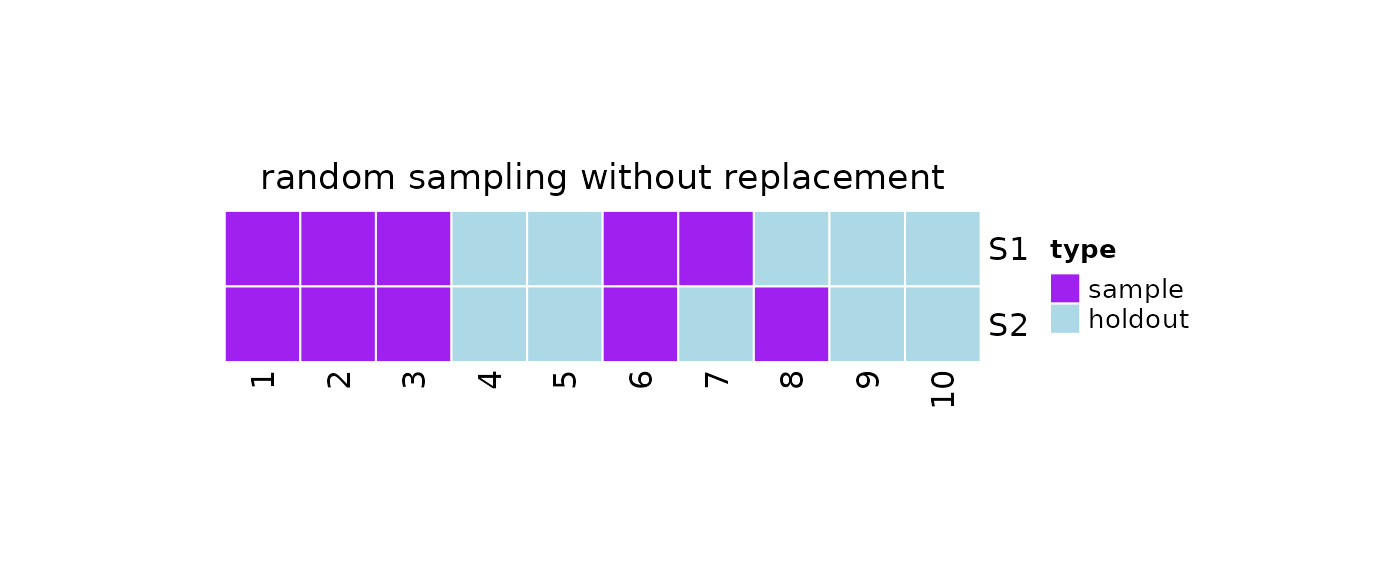

Stratified Random Sampling

Repeated stratified samples without replacement can be taken by using ?repeatedStratifiedSampleWithoutReplacement which accept a strata argument in input.

#Define strata
strata = c(rep("a", 3),rep("b", 6))

#Stratified sampling without replacement
repeatedStratifiedSampleWithoutReplacement(
  k = 2,
  strata = strata,
  n = 6
)
#> [[1]]
#> [1] 2 1 4 9 6 5
#> 
#> [[2]]
#> [1] 3 5 4 6 2 9

We can take repeated samples by using the ?resample function and setting method = 'stratified_rswor'.

#Stratified sampling without replacement
obj = resample(
  x = strata,
  n = 6,
  k = 2,
  method = 'stratified_rswor'
)

#Print
print(obj)
#> 
#> 2 samples taken from a population of 9 elements by using stratified
#> random sampling without replacement.
#> 
#>   sampleNumber          sample sampleSize holdoutSize
#> 1            1 1, 7, 5, 8, ...          6           3
#> 2            2 4, 8, 9, 2, ...          6           3

#Samples
getSamples(obj)
#> [[1]]
#> [1] 1 7 5 8 4 2
#> 
#> [[2]]
#> [1] 4 8 9 2 5 1

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> [1] 3 6 9
#> 
#> [[2]]
#> [1] 3 6 7

#Plot
plot(x = obj, strata = strata)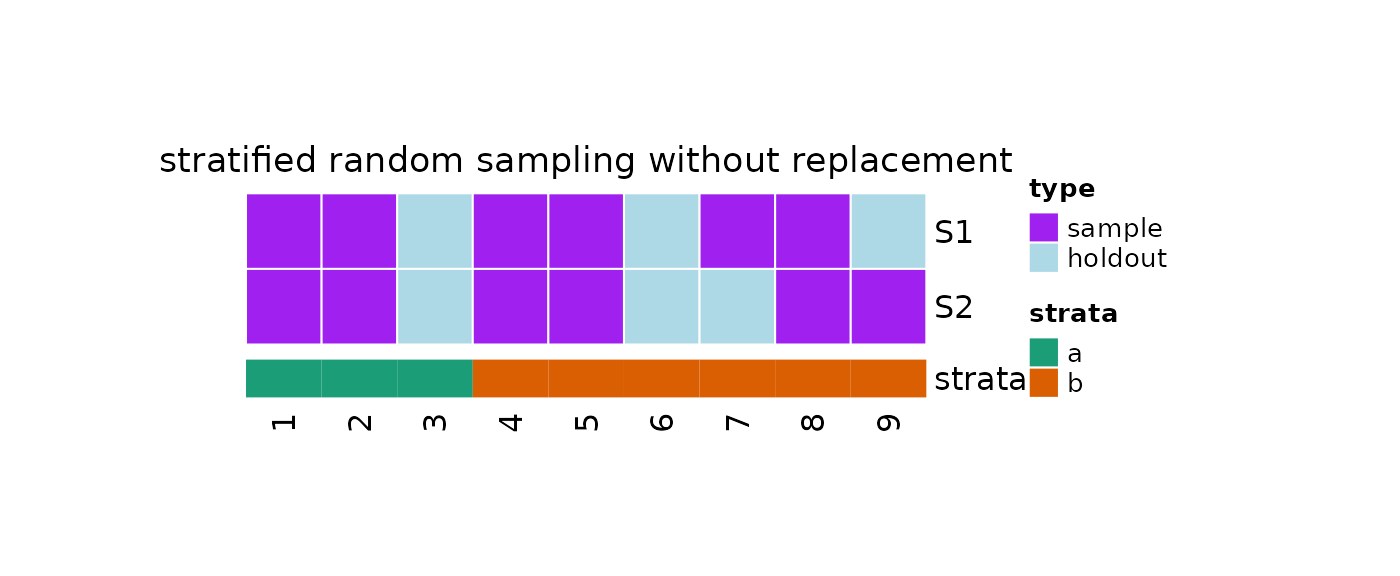

Balanced Random Sampling

Balanced sampling is a special case of stratified sampling used to ensure that subgroups of the population are equally represented in the taken sample.

Repeated balanced samples without replacement can be taken by using ?repeatedBalancedSampleWithoutReplacement:

#Define strata
strata = c(rep("a", 3),rep("b", 6))

#Check ratio
table(strata)/length(strata)
#> strata
#>         a         b 
#> 0.3333333 0.6666667

#Balanced sampling without replacement
s = repeatedBalancedSampleWithoutReplacement(
  k = 2,
  strata = strata,
  n = 6
)

#Check ratio in the samples
table(strata[s[[1]]])/length(strata[s[[1]]])
#> 
#>   a   b 
#> 0.5 0.5
table(strata[s[[2]]])/length(strata[s[[2]]])
#> 
#>   a   b 
#> 0.5 0.5

We can take repeated samples by using the ?resample function and setting method = 'balanced_rswor'.

#Balanced sampling without replacement
obj = resample(
  x = strata,
  n = 6,
  k = 2,
  method = 'balanced_rswor'
)

#Print
print(obj)
#> 
#> 2 samples taken from a population of 9 elements by using balanced
#> random sampling without replacement.
#> 
#>   sampleNumber          sample sampleSize holdoutSize
#> 1            1 8, 9, 3, 7, ...          6           3
#> 2            2 1, 5, 2, 3, ...          6           3

#Samples
getSamples(obj)
#> [[1]]
#> [1] 8 9 3 7 1 2
#> 
#> [[2]]
#> [1] 1 5 2 3 7 4

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> [1] 4 5 6
#> 
#> [[2]]
#> [1] 6 8 9

#Plot
plot(x = obj, strata = strata)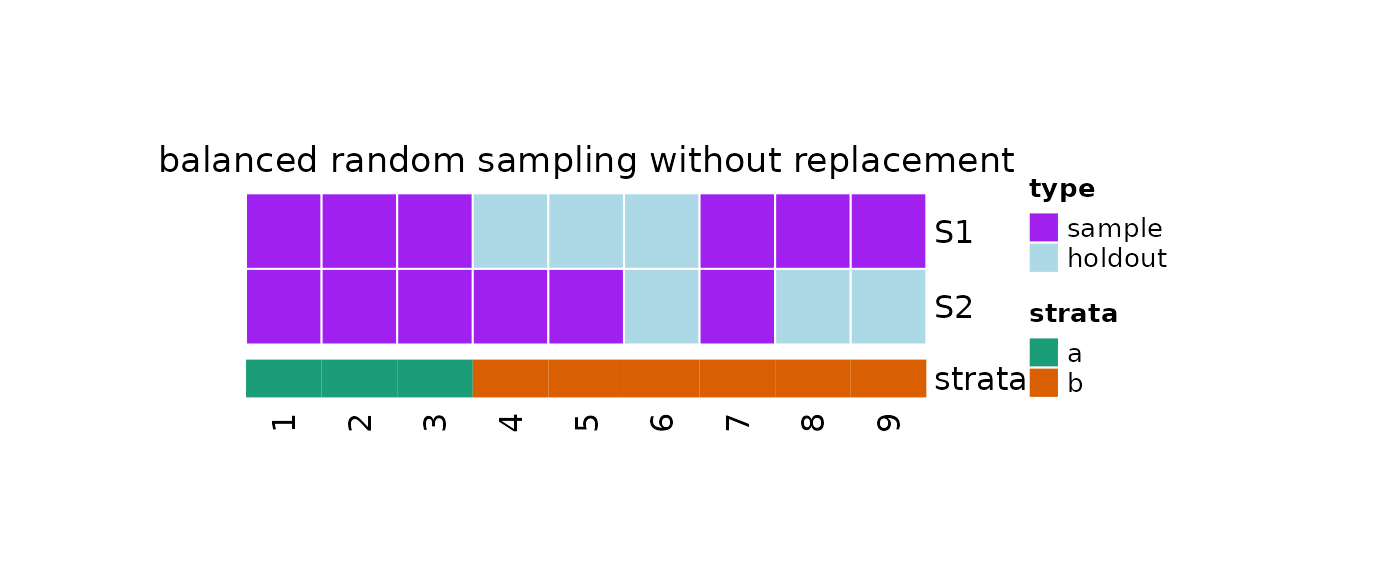

Permutation Sampling

We can take repeated permutation samples by using ?repeatedPermutationSample:

#Permutation sampling
repeatedPermutationSample(
  k = 2,
  N = 10
)
#> [[1]]
#>  [1]  3  6  8 10  2  1  5  9  7  4
#> 
#> [[2]]
#>  [1]  9  7  2  1  5  8  4  6  3 10

We can also use the ?resample function by setting method = 'permutation'.

#Permutation sampling
obj = resample(
  x = 10,
  k = 2,
  method = 'permutation'
)

#Print
print(obj)
#> 
#> 2 samples taken from a population of 10 elements by using permutation
#> sampling.
#> 
#>   sampleNumber          sample sampleSize holdoutSize
#> 1            1 10, 3, 5, , ...         10           0
#> 2            2 3, 9, 5, 4, ...         10           0

#Samples
getSamples(obj)
#> [[1]]
#>  [1] 10  3  5  8  7  6  4  2  9  1
#> 
#> [[2]]
#>  [1]  3  9  5  4  8 10  1  6  2  7

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> integer(0)
#> 
#> [[2]]
#> integer(0)

#Plot
plot(x = obj)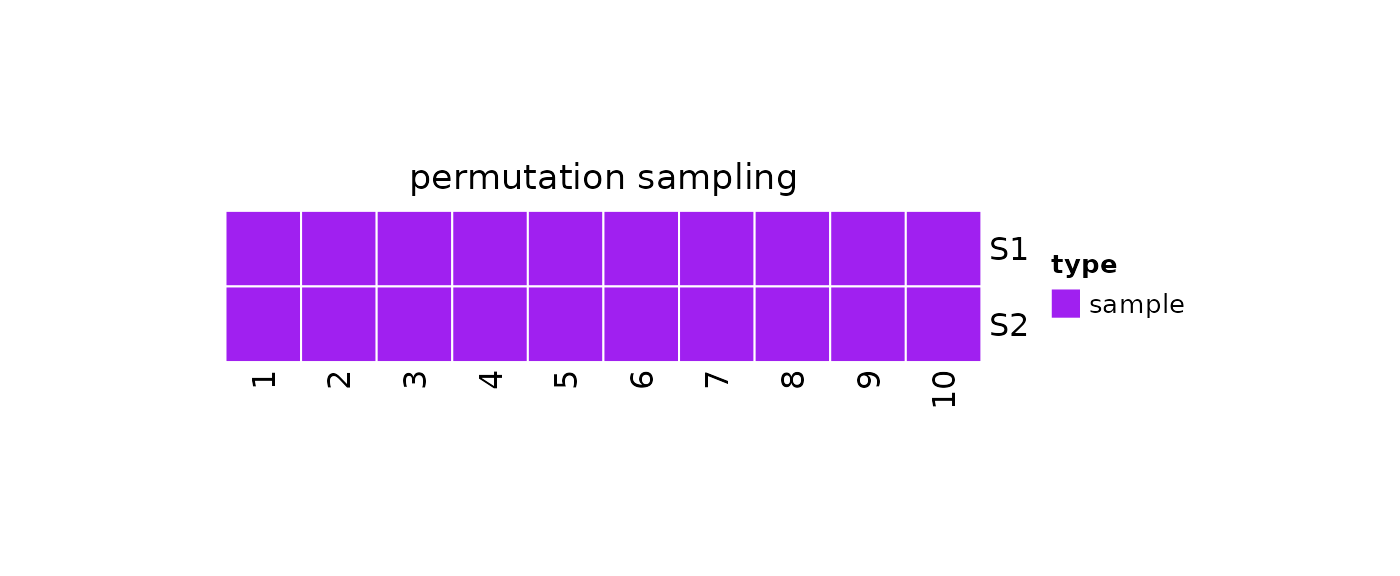

K-fold Sampling

The idea behind k-fold resampling is taken from k-fold cross-validation: k samples are taken from the population, so that the i-th sample is generated by removing the i-th fold from the population and merging the remaining k - 1 folds together.

We can take k samples via k-fold sampling by calling ?repeatedRandomKm1Folds. The function accepts two arguments in input:

• k: the number of folds
• N: the population size

?repeatedRandomKm1Folds returns a list of length k where each element is a sample obtained by merging k-1 folds together.

#K-1 folds sampling
repeatedRandomKm1Folds(
  N = 10,
  k = 3
)
#> [[1]]
#> [1] 1 2 3 4 7 8
#> 
#> [[2]]
#> [1]  3  4  5  6  8  9 10
#> 
#> [[3]]
#> [1]  1  2  5  6  7  9 10

We can take repeated samples by using the ?resample function and setting method = 'kfolds'.

#K-folds sampling
obj = resample(
  x = 10,
  k = 3,
  method = "kfolds"
)

#Print
print(obj)
#> 
#> 3 samples taken from a population of 10 elements by using random k-fold
#> sampling.
#> 
#>   sampleNumber          sample sampleSize holdoutSize
#> 1            1 1, 3, 4, 7, ...          6           4
#> 2            2 2, 3, 4, 5, ...          7           3
#> 3            3 1, 2, 5, 6, ...          7           3

#Samples
getSamples(obj)
#> [[1]]
#> [1]  1  3  4  7  8 10
#> 
#> [[2]]
#> [1] 2 3 4 5 6 8 9
#> 
#> [[3]]
#> [1]  1  2  5  6  7  9 10

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> [1] 2 5 6 9
#> 
#> [[2]]
#> [1]  1  7 10
#> 
#> [[3]]
#> [1] 3 4 8

#Plot
plot(obj)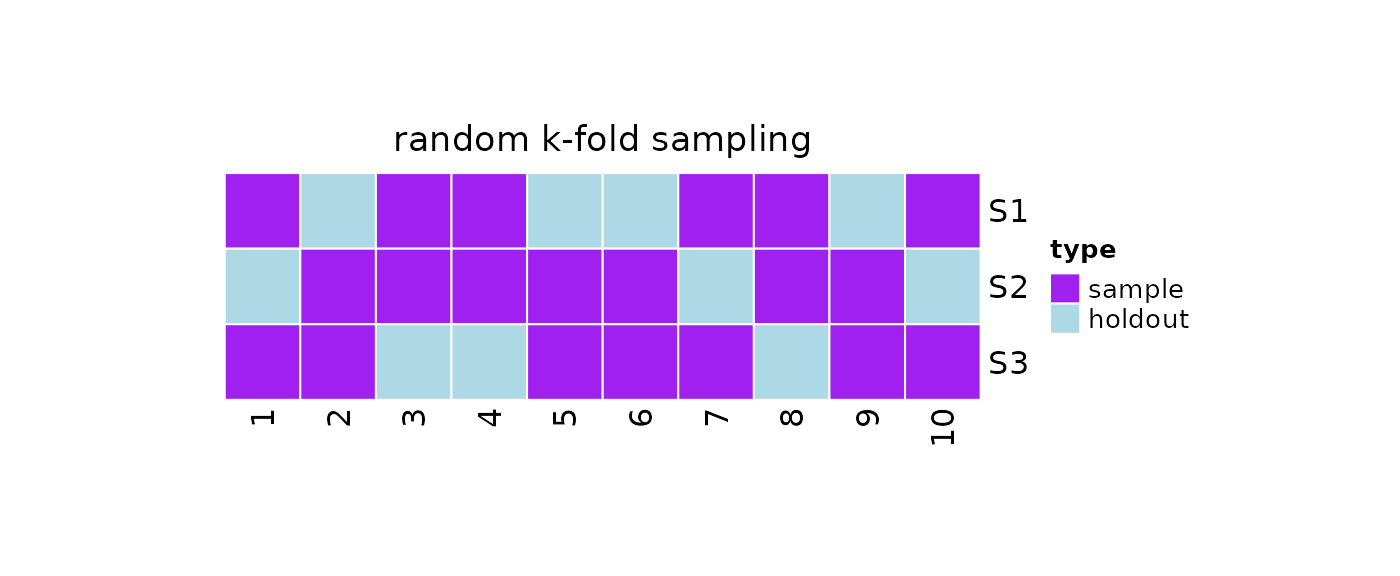

Stratified K-fold Sampling

We can take repeated stratified samples via stratified k-fold sampling by calling ?repeatedStratifiedKm1Folds.

?repeatedStratifiedKm1Folds assigns the population to k stratified folds and returns k samples made of elements from k-1 folds:

#Define strata
strata = c(rep("a", 3),rep("b", 6))

#Check ratio
table(strata)/length(strata)
#> strata
#>         a         b 
#> 0.3333333 0.6666667

#Assign data to 3 folds
i = repeatedStratifiedKm1Folds(
  strata = strata,
  k = 3
)

#Check folds
i
#> [[1]]
#> [1] 1 2 5 7 8 9
#> 
#> [[2]]
#> [1] 2 3 4 5 6 8
#> 
#> [[3]]
#> [1] 1 3 4 6 7 9

#Check ratio in the folds
table(strata[i[[1]]])/length(strata[i[[1]]])
#> 
#>         a         b 
#> 0.3333333 0.6666667
table(strata[i[[2]]])/length(strata[i[[2]]])
#> 
#>         a         b 
#> 0.3333333 0.6666667
table(strata[i[[3]]])/length(strata[i[[3]]])
#> 
#>         a         b 
#> 0.3333333 0.6666667

We can take repeated samples by using the ?resample function and setting method = 'stratified_kfolds'.

#Define strata
strata = c(rep("a", 3),rep("b", 6))

#Stratified k-folds sampling
obj = resample(
  x = strata,
  k = 3,
  method = "stratified_kfolds"
)

#Print
print(obj)
#> 
#> 3 samples taken from a population of 9 elements by using stratified
#> k-fold sampling.
#> 
#>   sampleNumber          sample sampleSize holdoutSize
#> 1            1 1, 3, 4, 5, ...          6           3
#> 2            2 1, 2, 5, 6, ...          6           3
#> 3            3 2, 3, 4, 7, ...          6           3

#Samples
getSamples(obj)
#> [[1]]
#> [1] 1 3 4 5 6 7
#> 
#> [[2]]
#> [1] 1 2 5 6 8 9
#> 
#> [[3]]
#> [1] 2 3 4 7 8 9

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> [1] 2 8 9
#> 
#> [[2]]
#> [1] 3 4 7
#> 
#> [[3]]
#> [1] 1 5 6

#Plot
plot(x = obj, strata = strata)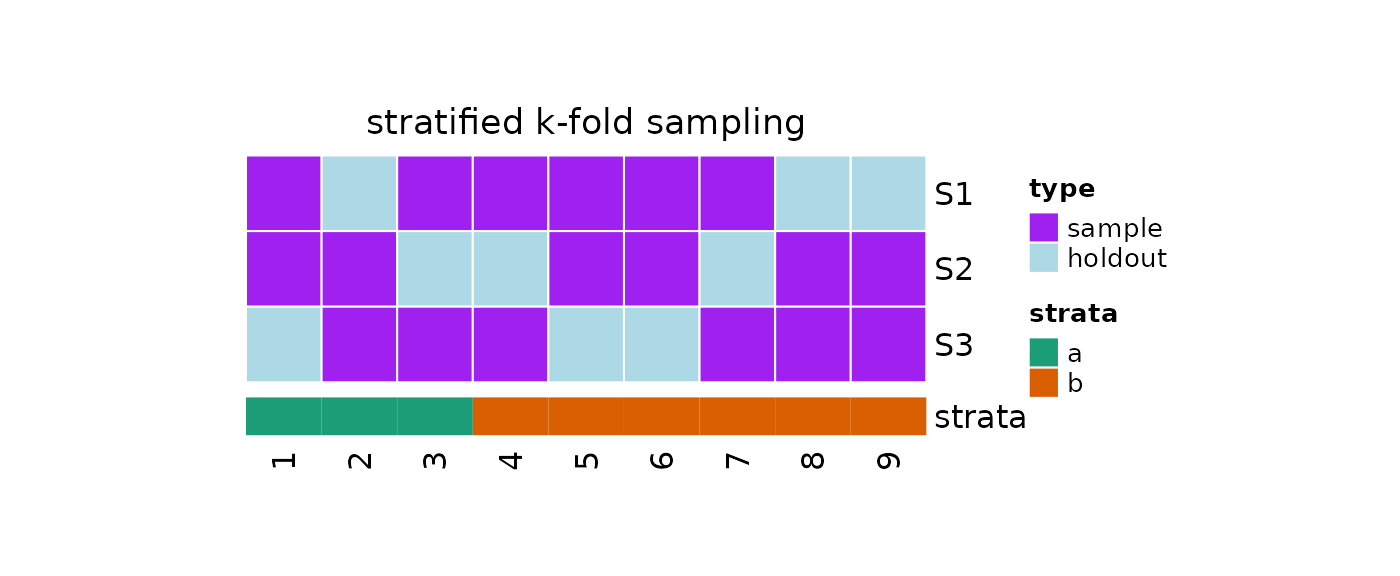

Balanced K-fold Sampling

We can take repeated balanced samples via balanced k-fold sampling by calling ?repeatedBalancedKm1Folds, which returns k samples made of elements from k-1 folds.

Internally, it uses ?balancedKFolds to assign the population to k balanced folds:

• If the population is balanced, each element in the population is assigned to one of the k folds so that the percentage of each stratum is preserved in each fold
• If the population is unbalanced and undersample = TRUE, the so-called random undersampling is adopted, i.e. the proportion of the strata in the population is adjusted by removing elements from the majority groups, so that each stratum is balanced

#Define balanced strata
strata = c(rep(1,6),rep(2,6))

#Check ratio
table(strata)/length(strata)
#> strata
#>   1   2 
#> 0.5 0.5

#Assign data to 3 folds and take a sample
i = repeatedBalancedKm1Folds(
  strata = strata,
  k = 3
)

#Check sample
i
#> [[1]]
#> [1]  1  2  4  5  7  8  9 10
#> 
#> [[2]]
#> [1]  2  3  4  6  8  9 11 12
#> 
#> [[3]]
#> [1]  1  3  5  6  7 10 11 12

#Check ratio in the sample
table(strata[i[[1]]])/length(strata[i[[1]]])
#> 
#>   1   2 
#> 0.5 0.5
table(strata[i[[2]]])/length(strata[i[[2]]])
#> 
#>   1   2 
#> 0.5 0.5
table(strata[i[[3]]])/length(strata[i[[3]]])
#> 
#>   1   2 
#> 0.5 0.5

#Define unbalanced strata
strata = c(rep(1,6),rep(2,12))

#Check ratio
table(strata)/length(strata)
#> strata
#>         1         2 
#> 0.3333333 0.6666667

#Assign data to 3 folds and take a sample
i = repeatedBalancedKm1Folds(
  strata = strata,
  k = 3,
  undersample = T
)
#Check folds
i
#> [[1]]
#> [1]  3  4  5  6  8 13 17 18
#> 
#> [[2]]
#> [1]  1  2  4  6  8 12 14 18
#> 
#> [[3]]
#> [1]  1  2  3  5 12 13 14 17
#> 
#> attr(,"removed.data")
#> [1]  7  9 10 11 15 16
#Check ratio in the folds
table(strata[i[[1]]])/length(strata[i[[1]]])
#> 
#>   1   2 
#> 0.5 0.5
table(strata[i[[2]]])/length(strata[i[[2]]])
#> 
#>   1   2 
#> 0.5 0.5
table(strata[i[[3]]])/length(strata[i[[3]]])
#> 
#>   1   2 
#> 0.5 0.5

We can take repeated samples by using the ?resample function.

#Define strata
strata = c(rep("a", 6),rep("b", 6))

#Balanced k-folds sampling (balanced population)
obj = resample(
  x = strata,
  k = 3,
  method = "balanced_kfolds"
)

#Print
print(obj)
#> 
#> 3 samples taken from a population of 12 elements by using balanced
#> k-fold sampling.
#> 
#>   sampleNumber          sample sampleSize holdoutSize
#> 1            1 1, 3, 4, 6, ...          8           4
#> 2            2 1, 2, 3, 5, ...          8           4
#> 3            3 2, 4, 5, 6, ...          8           4

#Samples
getSamples(obj)
#> [[1]]
#> [1]  1  3  4  6  7  9 10 12
#> 
#> [[2]]
#> [1]  1  2  3  5  7  8 11 12
#> 
#> [[3]]
#> [1]  2  4  5  6  8  9 10 11

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> [1]  2  5  8 11
#> 
#> [[2]]
#> [1]  4  6  9 10
#> 
#> [[3]]
#> [1]  1  3  7 12

#Plot
plot(x = obj, strata = strata)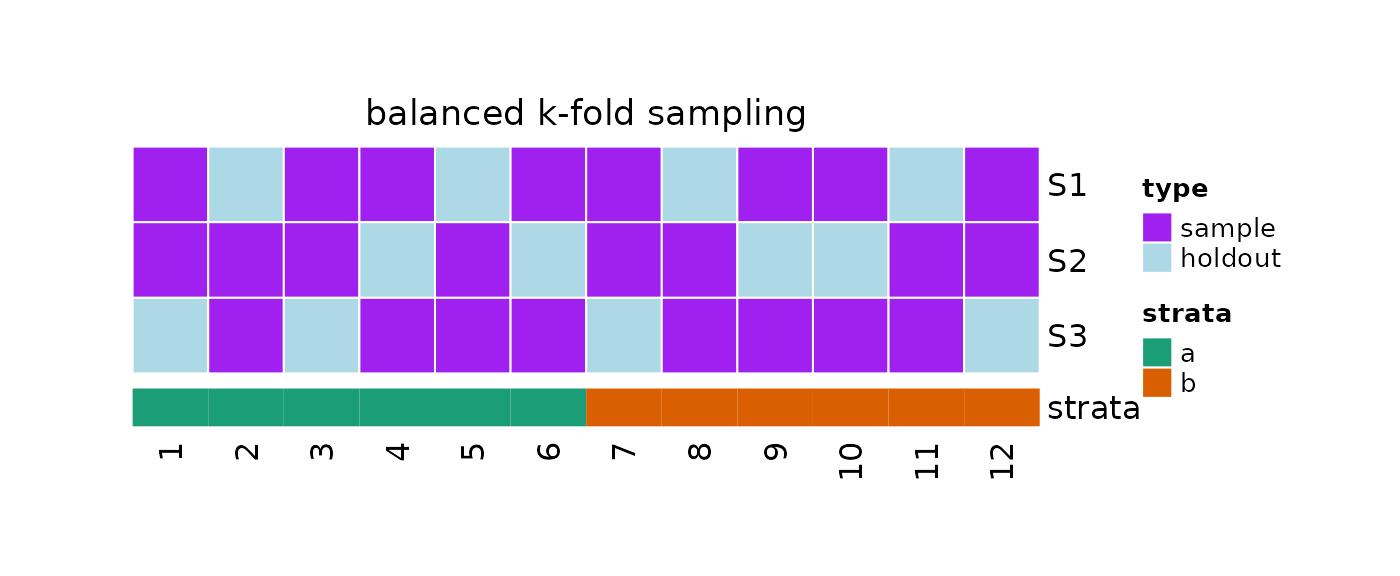

In case of unbalanced population, we can use the undersample argument.

#Define strata
strata = c(rep("a",6),rep("b",8))

#Balanced k-folds sampling (unbalanced population)
obj = resample(
  x = strata,
  k = 3,
  method = "balanced_kfolds",
  undersample = T
)

#Print
print(obj)
#> 
#> 3 samples taken from a population of 14 elements by using balanced
#> k-fold sampling.
#> 
#>   sampleNumber          sample sampleSize holdoutSize
#> 1            1 1, 2, 3, 4, ...          8           4
#> 2            2 3, 4, 5, 6, ...          8           4
#> 3            3 1, 2, 5, 6, ...          8           4

#Samples
getSamples(obj)
#> [[1]]
#> [1]  1  2  3  4  7 10 12 13
#> 
#> [[2]]
#> [1]  3  4  5  6  7  8 10 14
#> 
#> [[3]]
#> [1]  1  2  5  6  8 12 13 14

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> [1]  5  6  8 14
#> 
#> [[2]]
#> [1]  1  2 12 13
#> 
#> [[3]]
#> [1]  3  4  7 10

#Plot
plot(x = obj, strata = strata)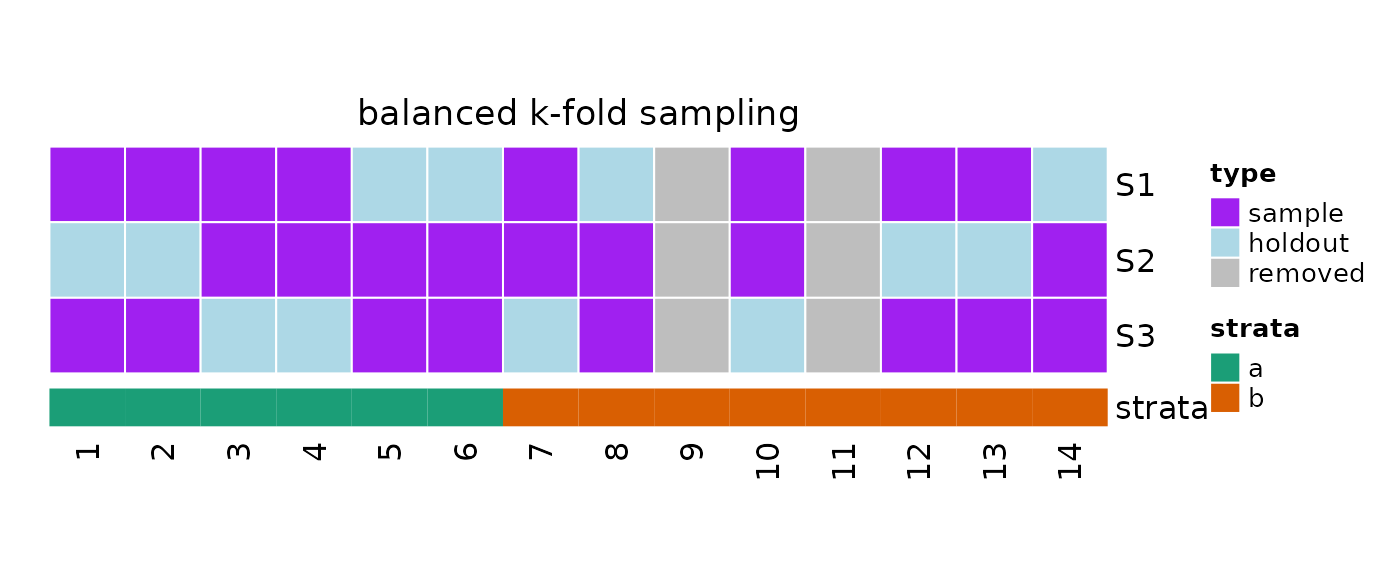

Leave-p-out Sampling

Leave-p-out resampling is an exhaustive resampling technique, in which samples of size p are repeatedly taken from the population until all the possible combinations of p elements are considered. These samples are then used as holdout data.

?repeatedLeavePOut returns a list of length \(\binom{N}{p}\) where each element is a sample obtained by removing the holdout data:

#Repeatedly sample leaving out p elements each time
repeatedLeavePOut(N = 5, p = 2)
#> [[1]]
#> [1] 3 4 5
#> 
#> [[2]]
#> [1] 2 4 5
#> 
#> [[3]]
#> [1] 2 3 5
#> 
#> [[4]]
#> [1] 2 3 4
#> 
#> [[5]]
#> [1] 1 4 5
#> 
#> [[6]]
#> [1] 1 3 5
#> 
#> [[7]]
#> [1] 1 3 4
#> 
#> [[8]]
#> [1] 1 2 5
#> 
#> [[9]]
#> [1] 1 2 4
#> 
#> [[10]]
#> [1] 1 2 3

In order to use the ?resample function, we need to set method = 'leave_p_out'.

#Leave-p-out sampling
obj = resample(
  x = 5,
  n = 2,
  method = "leave_p_out"
)

#Print
print(obj)
#> 
#> 10 samples taken from a population of 5 elements by using leave-p-out
#> sampling.
#> 
#>   sampleNumber  sample sampleSize holdoutSize
#> 1            1 3, 4, 5          3           2
#> 2            2 2, 4, 5          3           2
#> 3            3 2, 3, 5          3           2
#> 4            4 2, 3, 4          3           2
#> 5            5 1, 4, 5          3           2
#> ...

#Samples
getSamples(obj)
#> [[1]]
#> [1] 3 4 5
#> 
#> [[2]]
#> [1] 2 4 5
#> 
#> [[3]]
#> [1] 2 3 5
#> 
#> [[4]]
#> [1] 2 3 4
#> 
#> [[5]]
#> [1] 1 4 5
#> 
#> [[6]]
#> [1] 1 3 5
#> 
#> [[7]]
#> [1] 1 3 4
#> 
#> [[8]]
#> [1] 1 2 5
#> 
#> [[9]]
#> [1] 1 2 4
#> 
#> [[10]]
#> [1] 1 2 3

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> [1] 1 2
#> 
#> [[2]]
#> [1] 1 3
#> 
#> [[3]]
#> [1] 1 4
#> 
#> [[4]]
#> [1] 1 5
#> 
#> [[5]]
#> [1] 2 3
#> 
#> [[6]]
#> [1] 2 4
#> 
#> [[7]]
#> [1] 2 5
#> 
#> [[8]]
#> [1] 3 4
#> 
#> [[9]]
#> [1] 3 5
#> 
#> [[10]]
#> [1] 4 5

#Plot
plot(obj)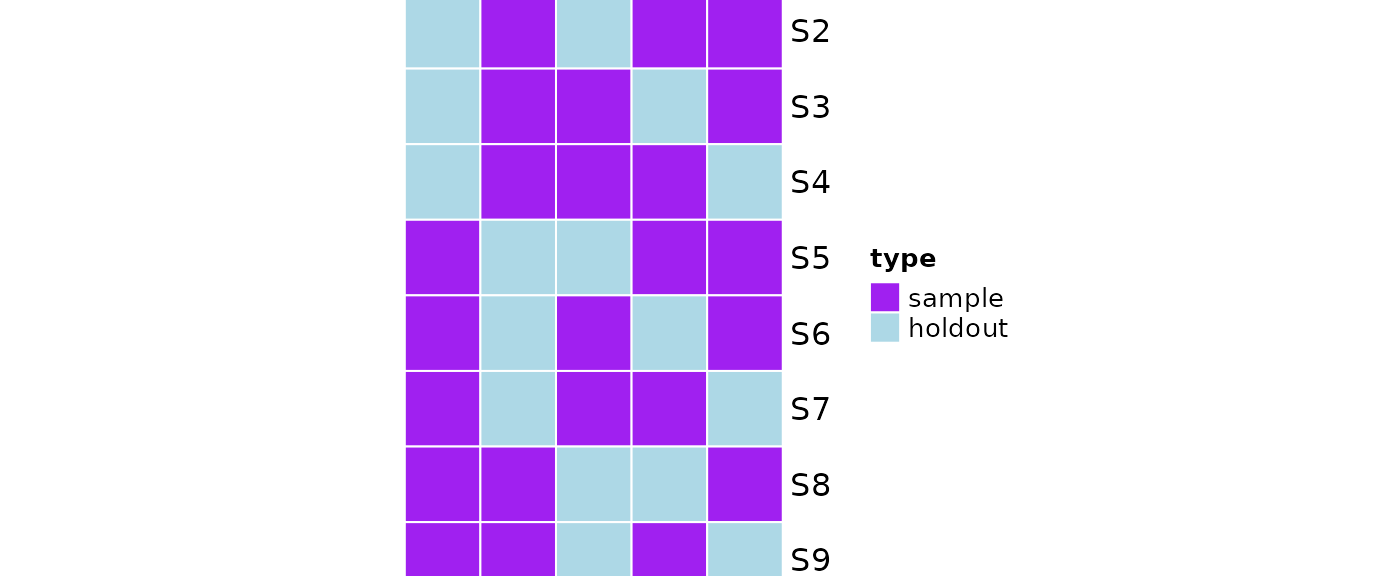

Leave-one-out Sampling

The leave-one-out is a particular case of the leave-p-out, where p = 1. Similarly to leave-p-out, leave-one-out resampling is an exhaustive resampling technique, in which samples of size 1 are repeatedly taken from the population until each element in the population is considered as the holdout data.

?repeatedLeaveOneOut returns a list of length N where each element is a sample obtained by removing the holdout data:

#Take one sample leaving out 1 element
repeatedLeaveOneOut(N = 5)
#> [[1]]
#> [1] 1 3 4 5
#> 
#> [[2]]
#> [1] 1 2 3 4
#> 
#> [[3]]
#> [1] 2 3 4 5
#> 
#> [[4]]
#> [1] 1 2 3 5
#> 
#> [[5]]
#> [1] 1 2 4 5

In order to use the ?resample function, we need to set method = 'leave_one_out'.

#Leave-one-out sampling
obj = resample(
  x = 5,
  method = "leave_one_out"
)

#Print
print(obj)
#> 
#> 5 samples taken from a population of 5 elements by using leave-one-out
#> sampling.
#> 
#>   sampleNumber     sample sampleSize holdoutSize
#> 1            1 1, 2, 4, 5          4           1
#> 2            2 1, 2, 3, 5          4           1
#> 3            3 1, 2, 3, 4          4           1
#> 4            4 1, 3, 4, 5          4           1
#> 5            5 2, 3, 4, 5          4           1

#Samples
getSamples(obj)
#> [[1]]
#> [1] 1 2 4 5
#> 
#> [[2]]
#> [1] 1 2 3 5
#> 
#> [[3]]
#> [1] 1 2 3 4
#> 
#> [[4]]
#> [1] 1 3 4 5
#> 
#> [[5]]
#> [1] 2 3 4 5

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> [1] 3
#> 
#> [[2]]
#> [1] 4
#> 
#> [[3]]
#> [1] 5
#> 
#> [[4]]
#> [1] 2
#> 
#> [[5]]
#> [1] 1

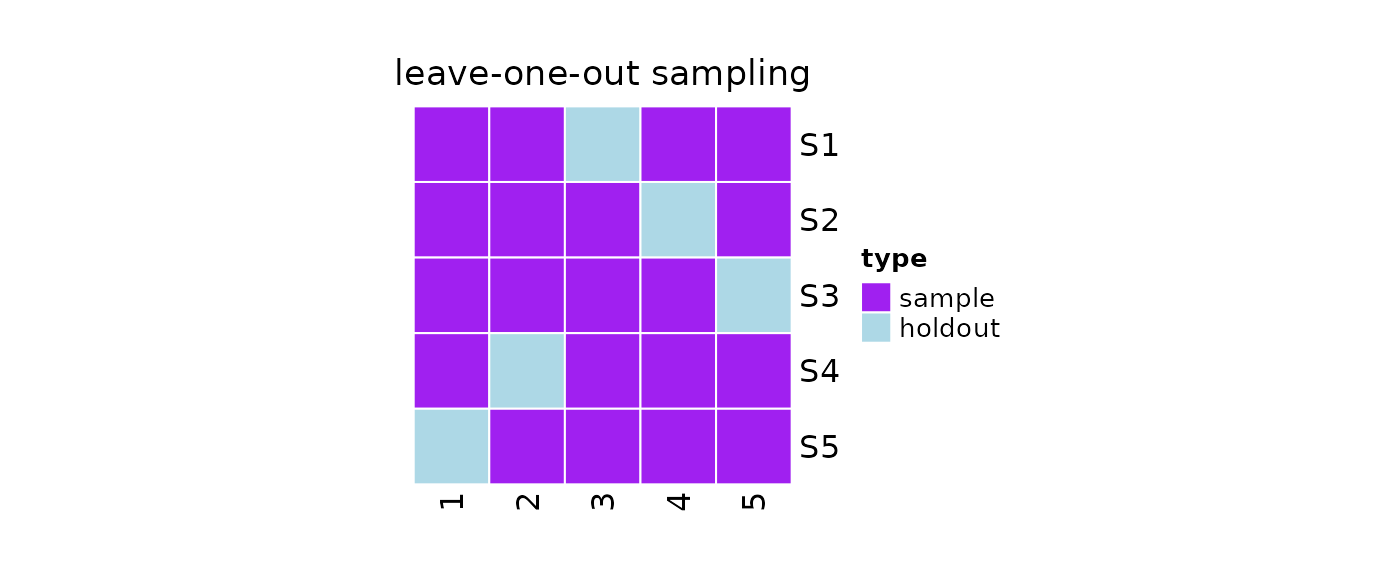
#Plot
plot(obj)