Skip to contents

An introduction to `resampling`

Source: vignettes/resampling.Rmd
resampling.Rmd

Introduction

resampling is an helpful package providing an easy way to take repeated samples (i.e. subsets of elements) from a population, here defined as a complete set of subjects of interest.

Resampling can be used for different purposes, including the estimation of the sampling distribution of an estimator, or the validation of predictive models in machine learning.

In this article, we show the main functions in resampling and a quick example. For further information, see:

Setup

Firstly, we need to load resampling and other needed R packages:

#resampling
library(resampling)

#Packages for visualisation
require(ComplexHeatmap, quietly = TRUE)
require(grid, quietly = TRUE)
require(RColorBrewer, quietly = TRUE)

Seed

Now we want to set a seed for the random number generation (RNG). In fact, different R sessions have different seeds created from current time and process ID by default, and consequently different simulation results. By fixing a seed we ensure we will be able to reproduce the results of this vignette. We can specify a seed by calling ?set.seed.

#Set a seed for RNG
set.seed(
  #A seed
  seed = 5381L,                   #a randomly chosen integer value
  #The kind of RNG to use
  kind = "Mersenne-Twister",      #we make explicit the current R default value
  #The kind of Normal generation
  normal.kind = "Inversion"       #we make explicit the current R default value
)

Sampling Methods

A list of currently supported sampling methods is available through the ?listAvailableSamplingMethods function call, which returns a table with two columns:

  • id: the id of the sampling method, to be used in the function calls
  • name: the name of the sampling method
#list sampling methods
sampling.methods = listAvailableSamplingMethods()

#print in table
knitr::kable(x = sampling.methods)
id name
rswor random sampling without replacement
srswor simple random sampling without replacement
stratified_rswor stratified random sampling without replacement
balanced_rswor balanced random sampling without replacement
permutation permutation sampling
kfolds random k-fold sampling
stratified_kfolds stratified k-fold sampling
balanced_kfolds balanced k-fold sampling
leave_p_out leave-p-out sampling
leave_one_out leave-one-out sampling
rswr random sampling with replacement
srswr simple random sampling with replacement
stratified_rswr stratified random sampling with replacement
balanced_rswr balanced random sampling with replacement
bootstrap ordinary bootstrap sampling

Sampling Functions

The name of the sampling functions can be retrieved by calling ?listSamplingFunctionNames.

#list sampling function names
sampling.function.names = listSamplingFunctionNames()

#print in table
knitr::kable(x = sampling.function.names)
id name
rswor sampleWithoutReplacement
srswor simpleRandomSampleWithoutReplacement
stratified_rswor stratifiedSampleWithoutReplacement
balanced_rswor balancedSampleWithoutReplacement
permutation permutationSample
kfolds randomKm1Folds
stratified_kfolds stratifiedKm1Folds
balanced_kfolds balancedKm1Folds
leave_p_out leavePOutSample
leave_one_out leaveOneOutSample
rswr sampleWithReplacement
srswr simpleRandomSampleWithReplacement
stratified_rswr stratifiedSampleWithReplacement
balanced_rswr balancedSampleWithReplacement
bootstrap bootstrapSample

Each function is documented. To learn more about a specific method it is possible to use the ? operator. For example, let’s check the function ?balancedSampleWithoutReplacement.

#See documentation
?balancedSampleWithoutReplacement

From the documentation, we can see that the function accepts three arguments in input:

  • strata: a vector of stratification variables
  • n: the sample size
  • prob: an optional vector of probabilities for obtaining the strata elements

Let’s draw a sample.

#Balanced sample without replacement
balancedSampleWithoutReplacement(
  strata = c(rep("a", 3),rep("b", 6)),
  n = 6
)
#> [1] 5 1 7 2 3 6

Resampling Functions

The name of the resampling functions can be retrieved by calling ?listResamplingFunctionNames.

#list resampling function names
resampling.function.names = listResamplingFunctionNames()

#print in table
knitr::kable(x = resampling.function.names)
id name
rswor repeatedSampleWithoutReplacement
srswor repeatedSimpleRandomSampleWithoutReplacement
stratified_rswor repeatedStratifiedSampleWithoutReplacement
balanced_rswor repeatedBalancedSampleWithoutReplacement
permutation repeatedPermutationSample
kfolds repeatedRandomKm1Folds
stratified_kfolds repeatedStratifiedKm1Folds
balanced_kfolds repeatedBalancedKm1Folds
leave_p_out repeatedLeavePOutSample
leave_one_out repeatedLeaveOneOutSample
rswr repeatedSampleWithReplacement
srswr repeatedSimpleRandomSampleWithReplacement
stratified_rswr repeatedStratifiedSampleWithReplacement
balanced_rswr repeatedBalancedSampleWithReplacement
bootstrap repeatedBootstrapSample

Each function is documented. To learn more about a specific method it is possible to use the ? operator. For example, let’s check the function ?repeatedStratifiedSampleWithoutReplacement.

#See documentation
?repeatedStratifiedSampleWithoutReplacement

From the documentation, we can see that this function takes repeated stratified samples without replacement from the population by repeatedly calling the ?stratifiedSampleWithoutReplacement sampling function. The ?stratifiedSampleWithoutReplacement help page reports that the function implements the so-called “proportionate allocation”, in which the proportion of the strata in the population is maintained in the samples.

?repeatedStratifiedSampleWithoutReplacement accepts 4 arguments in input:

  • k: the number of repeated samples to generate
  • strata: a vector of stratification variables
  • n: the sample size
  • prob: an optional vector of probabilities for obtaining the strata elements

Let’s draw 3 samples.

#Stratified random samples
repeatedStratifiedSampleWithoutReplacement(
  k = 3,
  strata = c(rep("a", 3),rep("b", 6)),
  n = 6
)
#> [[1]]
#> [1] 3 7 9 1 8 6
#> 
#> [[2]]
#> [1] 4 7 5 2 9 1
#> 
#> [[3]]
#> [1] 9 3 4 7 2 8

We can double-check that the proportion of the strata in the population is maintained in the samples:

#Define strata
strata = c(rep("a", 3),rep("b", 6))

#Check ratio
table(strata)/length(strata)
#> strata
#>         a         b 
#> 0.3333333 0.6666667

#Stratified random sample
i = repeatedStratifiedSampleWithoutReplacement(
  k = 2,
  strata = strata,
  n = 3
)

#Check indices
i
#> [[1]]
#> [1] 5 3 4
#> 
#> [[2]]
#> [1] 5 3 4

#Check ratio
table(strata[i[[1]]])/length(strata[i[[1]]])
#> 
#>         a         b 
#> 0.3333333 0.6666667
table(strata[i[[2]]])/length(strata[i[[2]]])
#> 
#>         a         b 
#> 0.3333333 0.6666667

resample Function

Instead of using the different resampling functions, we can use ?resample which provides a unique interface to the various resampling methods. The parameters in input are:

  • x: either an integer representing the population size, or a vector of stratification variables
  • n: either the sample size or the number of elements to holdout
  • k: the number of repeated samples to generate. It is used as the number of folds in k-fold sampling
  • method: one of the supported sampling techniques. See ?listAvailableSamplingMethods
  • prob: (optional) vector of probability weights for obtaining the elements from the population. If provided, its length must match the population size
  • undersample: logical, whether to remove elements from the population in order to try to obtain balanced data

The function returns an object of class ?resampling, which represents a series of samples repeatedly taken from a population.

resampling S3 Class

The resampling class represents a series of samples repeatedly taken from a population. A resampling object is a list consisting of 4 elements:

  • method: the id of the used sampling method
  • N: the size of the population from which the samples were taken. Elements in the population have index from 1 to N
  • removed: (optional) vector of indices of elements removed from the population before taking the samples
  • samples: list of samples repeatedly taken from the population. Each element of the list is an integer vector containing the indices of the elements sampled from the population

Functions to facilitate access to the data stored in a resampling object are available:

Two other useful functions are print and plot:

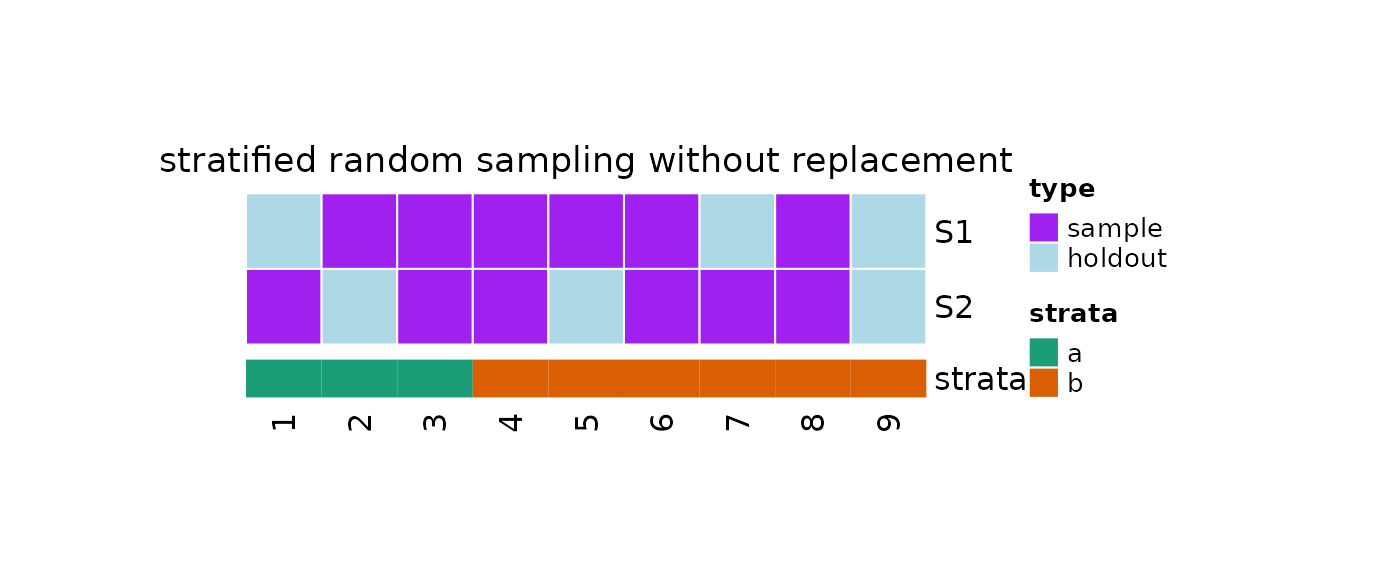
Take Repeated Samples

Now let’s use the ?resample function to take repeated samples from a population of 9 elements made of 2 groups (group a and group b).

#Define strata
strata = c(rep("a", 3),rep("b", 6))

For this example, we want to use stratified sampling without replacement. If we look at the table returned by ?listAvailableSamplingMethods, we can see that the id for stratified sampling without replacement is stratified_rswor. We can use this value as the method argument in ?resample:

#Random sampling without replacement
obj = resample(
  x = strata,
  n = 6,
  k = 2,
  method = "stratified_rswor"
)

We can check if the returned object is of class resampling:

#Is obj of class `resampling`?
is.resampling(obj)
#> [1] TRUE

Now, we could print a summary:

#Print
print(obj)
#> 
#> 2 samples taken from a population of 9 elements by using stratified
#> random sampling without replacement.
#> 
#>   sampleNumber          sample sampleSize holdoutSize
#> 1            1 3, 5, 8, 2, ...          6           3
#> 2            2 1, 8, 4, 3, ...          6           3

We can use ?getSamples to extract the taken samples from the resampling object:

#Samples
getSamples(obj)
#> [[1]]
#> [1] 3 5 8 2 6 4
#> 
#> [[2]]
#> [1] 1 8 4 3 7 6

The holdout data can be obtained by using ?getHoldOutSamples:

#Holdout Data
getHoldOutSamples(obj)
#> [[1]]
#> [1] 1 7 9
#> 
#> [[2]]
#> [1] 2 5 9

We can also plot our object as an heatmap:

#Plot
plot(
  x = obj, 
  strata = strata
)