Skip to contents

An introduction to `renoir`

Source: vignettes/renoir.Rmd
renoir.Rmd

Introduction

renoir is a package that evaluates a chosen machine learning methodology via a multiple random sampling approach spanning different training-set sizes.

renoir has been developed thinking about a teaching/learning abstraction. There are two main actors in the renoir framework: the learner, and the evaluator.

  • The learner represents the learning method under assessment and is linked to the ?Learner class.
  • The evaluator is responsible for the evaluation procedure, i.e. the assessment of the performance of the learner via multiple random sampling, and it is related to the ?Evaluator class.

The example in the Quick Start will help you in familiarizing with these concepts.

Quick Start

In this section we will briefly go over the main functions, basic operations and outputs.

First, we load the renoir package:

library(renoir)
#> Warning: package 'Matrix' was built under R version 4.2.3

For this brief example, we decided to show the functionality of renoir for a classification problem. Let us load a set of data for illustration:

data(binomial_example)

The command loads an input matrix x and a response vector y from a saved R data archive.

Now we want to set a seed for the random number generation (RNG). In fact, different R sessions have different seeds created from current time and process ID by default, and consequently different simulation results. By fixing a seed we ensure we will be able to reproduce the results of this example. We can specify a seed by calling ?set.seed.

#Set a seed for RNG
set.seed(
  #A seed
  seed = 5381L,                   #a randomly chosen integer value
  #The kind of RNG to use
  kind = "Mersenne-Twister",      #we make explicit the current R default value
  #The kind of Normal generation
  normal.kind = "Inversion"       #we make explicit the current R default value
)

As reported in the Introduction, the main actors in renoir are the ?Learner and ?Evaluator classes, and these are also the main elements we need to set up before running our analysis.

Supported Methods

Learning Methods

Let us start with the ?Learner. A ?Learner is a container for the different essential elements of the learning methodology we want to evaluate. In this example, we will focus on just three elements, i.e. the learning procedure, the sampling approach, the performance metric.

As a first step, we need to select a learning methodology to evaluate. A list of supported methods is available through the ?list_supported_learning_methods function call.

#list methods
learning.methods = list_supported_learning_methods()

#print in table
knitr::kable(x = learning.methods)
id method default_hyperparameters
lasso generalized linear model via L1 penalized maximum likelihood (lasso penalty) lambda
ridge generalized linear model via L2 penalized maximum likelihood (ridge penalty) lambda
elasticnet generalized linear model via L1/L2 penalized maximum likelihood (elasticnet penalty) lambda, ….
relaxed_lasso generalized linear model via L1 penalized maximum likelihood (relaxed lasso penalty) lambda, ….
relaxed_ridge generalized linear model via L2 penalized maximum likelihood (relaxed ridge penalty) lambda, ….
relaxed_elasticnet generalized linear model via L1/L2 penalized maximum likelihood (relaxed elasticnet penalty) lambda, ….
randomForest random forest ntree
gbm generalized boosted model eta, ntree
linear_SVM linear support vector machine cost
polynomial_SVM polynomial support vector machine cost, ga….
radial_SVM radial support vector machine cost, gamma
sigmoid_SVM sigmoid support vector machine cost, gamma
linear_NuSVM linear nu-type support vector machine nu
polynomial_NuSVM polynomial nu-type support vector machine nu, gamm….
radial_NuSVM radial nu-type support vector machine nu, gamma
sigmoid_NuSVM sigmoid nu-type support vector machine nu, gamma
gknn generalized k-nearest neighbours model k
nsc nearest shrunken centroid model threshold

For this example, we choose a generalized linear model via L1 penalty (the lasso) as learning method. From the table, we can see that the default hyperparameter of the method is lambda.

Sampling Methods

Now we want to select a sampling procedure to use for the tuning of the hyperparameter. A list of supported sampling methods is available through the ?list_supported_sampling_methods function call.

#list methods
sampling.methods = list_supported_sampling_methods()

#print in table
knitr::kable(x = sampling.methods)
id name supported
random random sampling without replacement stratification, balance
bootstrap random sampling with replacement stratification, balance
cv cross-validation stratification

We can see how renoir currently supports three sampling scheme: random sampling with and without replacement, and cross-validation. They all provide options for a stratified approach, where a so-called ‘proportionate allocation’ is attempted to maintain the proportion of the strata in the samples as is in the population. On the other hand, only random sampling and bootstrap allow for balancing, meaning that the proportion of strata in the sample is attempted to be balanced.

For this example, we decided to tune the parameter via a stratified 10-fold cross-validation.

Scoring Methods

Finally, we want to choose a performance metric to assess the models during the tuning. A list of supported scoring metrics is available through the ?list_supported_performance_metrics function call.

#list metrics
performance.metrics = list_supported_performance_metrics()

#print in table
knitr::kable(x = performance.metrics)
id name problem
mae Mean Absolute Error regression
mape Mean Absolute Percentage Error regression
mse Mean-squared Error regression
rmse Root-mean-square Error regression
msle Mean-squared Logarithmic Error regression
r2 R2 regression
class Misclassification Error classification
acc Accuracy classification
auc AUC classification
f1s F1 Score classification
fbeta F-beta Score classification
precision Precision classification
sensitivity Sensitivity classification
jaccard Jaccard Index classification

We can see that the ?list_supported_performance_metrics function reported the performance metrics for both regression and classification problems. Let us refine our search by listing the supported metrics for the binomial response type only. We can do this by providing the resp.type argument to the function as shown below.

#list metrics
performance.metrics = list_supported_performance_metrics(resp.type = "binomial")

#print in table
knitr::kable(x = performance.metrics)
id name problem
class Misclassification Error classification
acc Accuracy classification
auc AUC classification
f1s F1 Score classification
fbeta F-beta Score classification
precision Precision classification
sensitivity Sensitivity classification
jaccard Jaccard Index classification

As expected, now only the metrics for classification problems are listed. Let us select the misclassification error (also called classification error rate) as performance metric.

So, overall we want to train a model with a lasso, tuning the hyperparameter lambda via 10-fold cross-validation and by using the misclassification error to assess the performance of the models.

Main Elements

Learner

Since the lasso is a renoir built-in method, we can create the related ?Learner object with a single command.

#Learner
learner <- Learner(
  #Learning method
  id        = "lasso",    #generalised linear model with penalization
  #Response type
  resp.type = "binomial",
  #Sampling strategy
  strata    = y,          #by providing a strata we select the stratified approach
  sampling  = "cv",       #cross-validation
  k         = 10L,        #10-fold
  #Performance metric
  score     = "class"     #classification error rate
)

Here above we used the simplified interface for the constructor, which is internally creating the different needed elements. If we want a fine-grained setting we can use the alternative interface as shown below.

#Learner
learner <- Learner(
  #Trainer
  trainer = Trainer(id = "lasso"),   #generalised linear model with penalization
  
  #Tuner
  tuner = Tuner(
    sampler = Sampler(               #A Sampler contains info for the sampling strategy 
      method = "cv",                 #cross-validation
      k = 10L,                       #10-fold
      strata = y                     #by providing a strata we select the stratified approach
    )
  ),
  
  #Predictor
  forecaster = Forecaster(id = "lasso"),
  
  #Performance metric
  scorer     = Scorer(               
    id = "class",                    #classification error rate
    resp.type = "binomial"),
  
  #Select one model from a list
  selector   = Selector(id = "lasso"),
  
  #Record features presence in a model
  recorder   = Recorder(id = "lasso"),
  
  #Assign a mark to each feature
  marker     = Marker(id = "lasso")
)

We are not going into details in this example, however you should note that the sampling procedure is set up by creating an object of class ?Sampler, while an object of class ?Scorer can be used to define the performance metric.

Evaluator

Now we need to set up the ?Evaluator. Objects of this class contains the infrastructure for the evaluation procedure, which mainly consists in the sampling strategy to adopt and the metric to compute as estimate of the learning method performance. We can easily set up the sampling strategy and the performance metric by creating objects of class ?Sampler and ?Scorer, respectively as shown below.

#Evaluator
evaluator = Evaluator(
  #Sampling strategy: stratified random sampling without replacement
  sampler = Sampler(               #Sampler object
    method = "random",             #random sampling without replacement
    k = 10L,                        #k repeats
    strata = y,                    #stratified
    N = as.integer(length(y))      #population size
  ),

  #Performance metric
  scorer  = Scorer(id = "class"),
)

Run Evaluation

Now that our main actors are set, we can run the analysis. renoir provides a single command for this purpose, the ?renoir function. The essential required elements are a ?Learner, an ?Evaluator, the predictor matrix x, the response variable y, and the response type resp.type. Since our chosen learning method has one hyperparameter (lambda), we also need to provide a hyperparameters element, where we supply our sequence of values that will be used during the tuning of the model.

#Renoir
renoirl = renoir(
  #Learn
  learner   = learner,                  #a Learner object

  #Evaluate
  evaluator = evaluator,                #an Evaluator object

  #Data for tuning
  hyperparameters = list(               #the hyperparameter we
    lambda = 10^seq(3, -2, length=100)  #want to tune (for the
  ),                                    #lasso is lambda)
  
  #Data for training
  x         = x,                        #the predictor matrix
  y         = y,                        #the response variable
  resp.type = "binomial"                #the response type
)

Explore Results

renoirl is a list containing two elements of class ?Renoir, each providing all the relevant information of the evaluation procedure. There are two elements because renoir tries to select two different final configurations during the tuning procedure: one configuration (called opt) is the configuration having a mean performance during the chosen repeated sampling procedure which is the optimum value when compared across all the others, e.g. the configuration with the minimal classification error rate; the other (called 1SE) is the configuration resulting from the application of the so-called one standard error rule which consists in selecting the most parsimonious model having a mean performance within one standard error from the optimum.

Summary Table

Various methods are provided for the ?Renoir object. For example, we can produce a summary data.frame containing the evaluation of the lasso across the different training-set sizes by executing the ?summary_table command:

#get the summary
s = summary_table(object = renoirl[[1]])

#print in table
DT::datatable(
  data = s,                  #data to table
  rownames           = F,    #don't show row names
  options = list(           
    lengthMenu = list(       #length of the menu
      c(3, 5, 10),           #set 3 as the minimum 
      c(3, 5, 10)),          #number of shown entries
    scrollX = T),            #enable horizontal scrolling
  width = "100%",            #width size
  height = "auto"            #height size
)

Visualization

We can also visualize the results by executing the ?plot function. For example, let us plot the results of the evaluation when considering the full set of data:

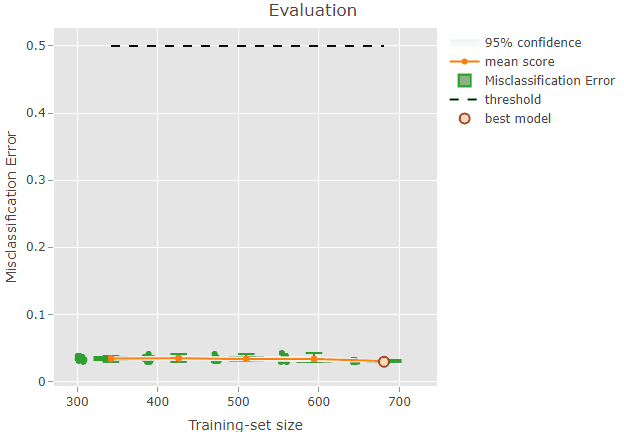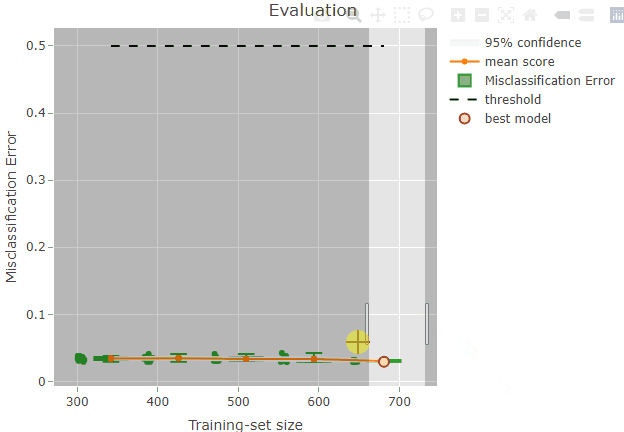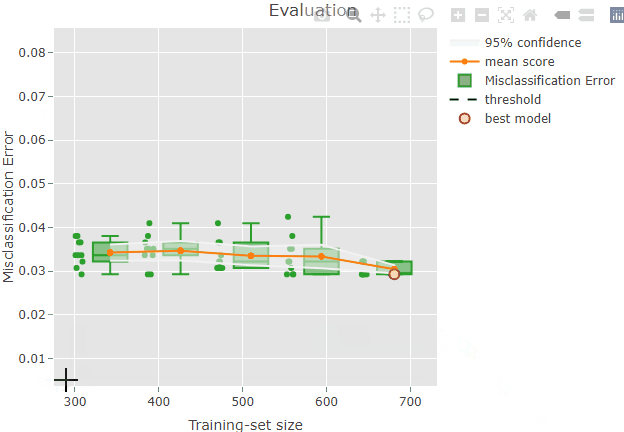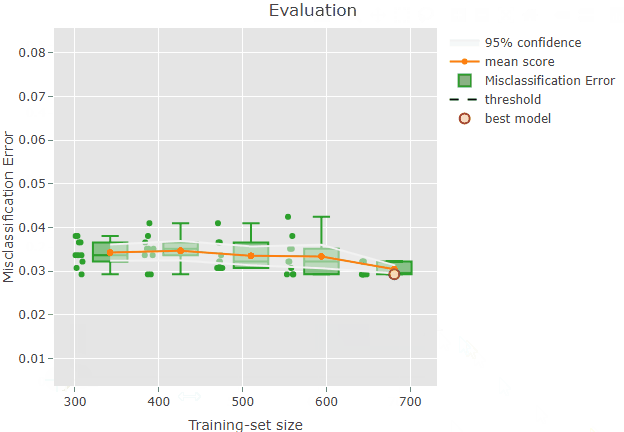
plot(x = renoirl[[1]], measure = "class", set = "full")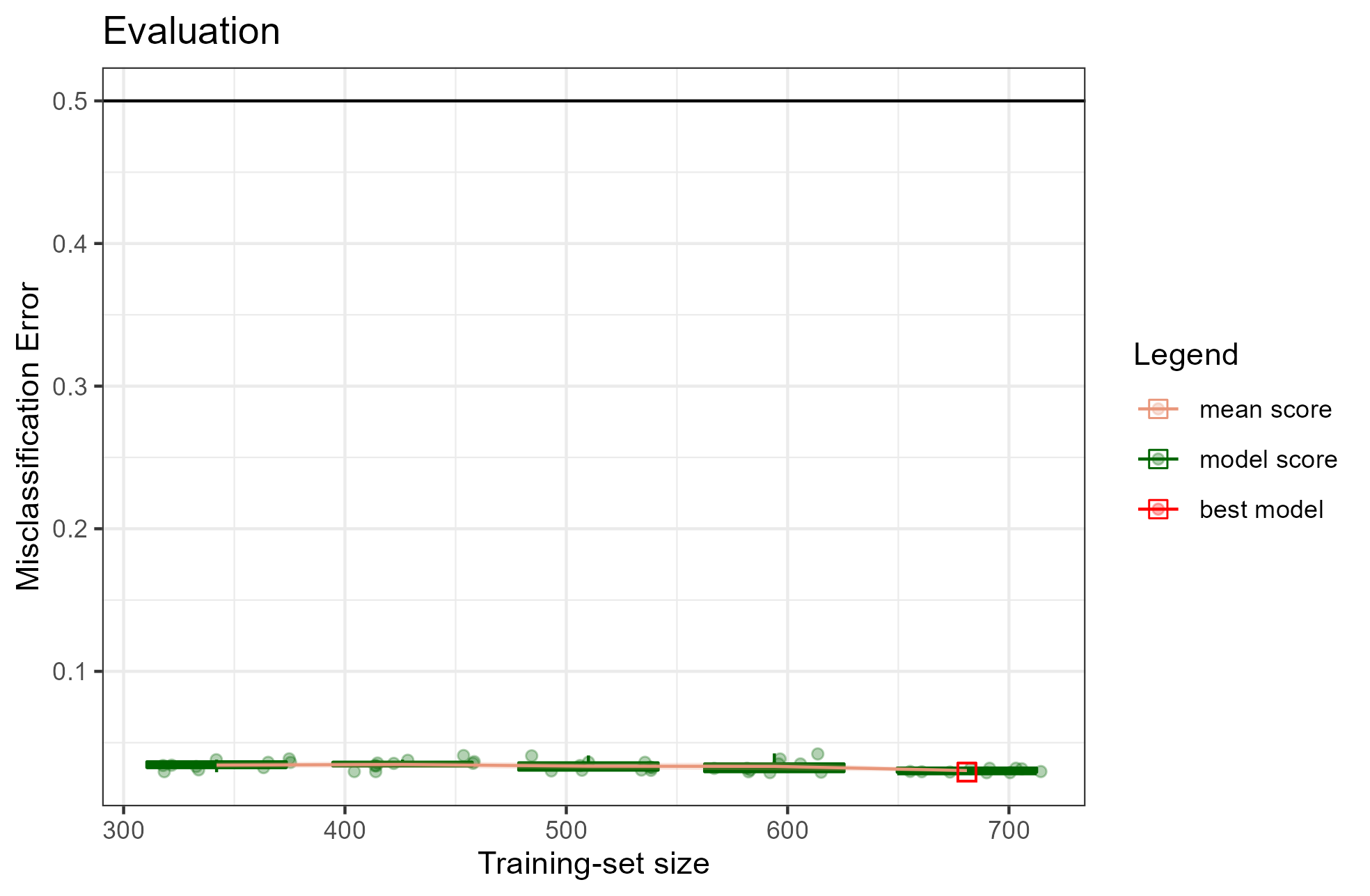

Each circle corresponds to the performance of a trained model. The mean performance metric (i.e. the mean misclassification error) computed from the model performance scores for each training-set size is shown as an orange line, while the related confidence intervals are drawn as bands around the mean. The red square represents the overall best model selected via an internal procedure: for example, when considering the misclassification error, renoir selects a potential best model by choosing the model with the minimal score across all the models fitted using the training-set size showing the lowest upper bound of the 95% CI. In this example, the plot shows a quite constant mean score around 0.03 across training-set sizes, indicating a good performance of the classifier.

To facilitate the inspection of the results, it is also possible to produce an interactive plot by setting the argument interactive = TRUE in the ?plot command.

plot(x = renoirl[[1]], measure = "class", set = "full", interactive = TRUE)

The plot can now be zoomed by selecting an area:

Some information is also shown when hoovering over a plot element. For example, if you try to hoover over the red dot representing the best model you should be able to see something like this:

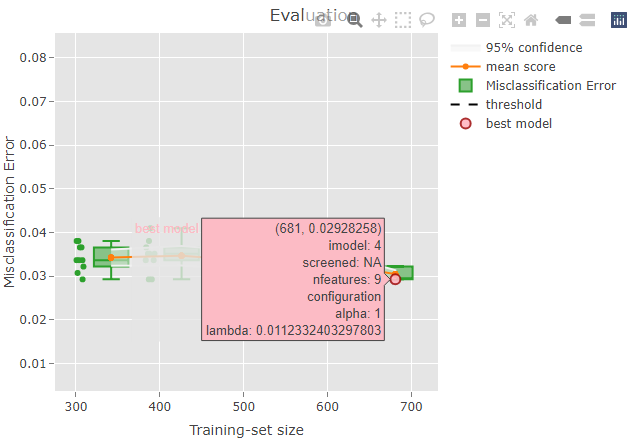
The top row indicates the position on the x and y axes: the selected model has a training-set size of 681 and a misclassification error of 0.029. Please, note that the circles are slightly jittered from their position for a clearer plot, but the values reported while hoovering are correct. The second row is reporting the iteration index corresponding to the model: in this case, the 4th model trained during the repeated sampling procedure was selected as the best model. No supervised screening was performed, and the model contains 9 features. Finally, the value of lambda resulted from the tuning and that was used to train the final model is reported.

Models

Now that we have identified a potential model of interest, we may want to extract from the Renoir object. We can easily do it by using the ?get_model command. It requires three arguments:

  • object: an object of class Renoir
  • n: the sample size to consider
  • index: index of the model to select
m = get_model(
  object = renoirl[[1]], # Renoir object
  n = 681,               # Training-set size
  index = 4              # Model index
)

The model can now be used for further analysis. For example, we may want to use it for prediction.

newy = forecast(
  models = m,
  newx = x,
  type = 'class'
)

table(newy)
#> newy
#>    benign malignant 
#>       446       237

We could also be interested in the non-zero features of the model. For this task, we can use the ?features command. The two main arguments are:

  • object: an object of class Trained or Tuned
  • type: a string indicating whether to return all features or just the ones with non-zero coefficients (nonzero).
feats = features(object = m, type = "nonzero")

unlist(feats)
#> [1] "Cl.thickness"    "Cell.size"       "Cell.shape"      "Marg.adhesion"  
#> [5] "Epith.c.size"    "Bare.nuclei"     "Bl.cromatin"     "Normal.nucleoli"
#> [9] "Mitoses"

Global Features Importance

Finally, we might want to investigate the features importance across all the models. We easily extract this by using the ?signature command and specifying the performance metric to consider and the set.

featimp = renoir::signature(object = renoirl[[1]], measure = "class", set = "test")
featimp
#>                         V1
#> Cl.thickness    0.26128899
#> Cell.size       0.29092229
#> Cell.shape      0.31327881
#> Marg.adhesion   0.13525482
#> Epith.c.size    0.13296202
#> Bare.nuclei     0.31922395
#> Bl.cromatin     0.25066154
#> Normal.nucleoli 0.22569934
#> Mitoses         0.03448299